Радиальная симметрия
Содержание:
Биология
В биологии о радиальной симметрии говорят, когда через трёхмерное существо проходят одна или более осей симметрии. При этом радиальносимметричные животные могут и не иметь плоскостей симметрии. Так, у сифонофоры Velella имеется ось симметрии второго порядка и нет плоскостей симметрии.
Обычно через ось симметрии проходят две или более плоскости симметрии. Эти плоскости пересекаются по прямой — оси симметрии. Если животное будет вращаться вокруг этой оси на определённый градус, то оно будет отображаться само на себе (совпадать само с собой).
Таких осей симметрии может быть несколько (полиаксонная симметрия) или одна (монаксонная симметрия). Полиаксонная симметрия распространена среди протистов (например, радиолярий).
Как правило, у многоклеточных животных два конца (полюса) единственной оси симметрии неравноценны (например, у медуз на одном полюсе (оральном) находится рот, а на противоположном (аборальном) — верхушка колокола. Такая симметрия (вариант радиальной симметрии) в сравнительной анатомии называется одноосно-гетеропольной. В двухмерной проекции радиальная симметрия может сохраняться, если ось симметрии направлена перпендикулярно к проекционной плоскости. Иными словами, сохранение радиальной симметрии зависит от угла наблюдения.
Радиальная симметрия характерна для многих стрекающих, а также для большинства иглокожих. Среди них встречается так называемая пентасимметрия, базирующаяся на пяти плоскостях симметрии. У иглокожих радиальная симметрия вторична: их личинки двустороннесимметричны, а у взрослых животных наружная радиальная симметрия нарушается наличием мадрепоровой пластинки.
Кроме типичной радиальной симметрии существует двулучевая радиальная симметрия (две плоскости симметрии, к примеру, у гребневиков). Если плоскость симметрии только одна, то симметрия билатеральная (такую симметрию имеют животные из группы Bilateria).
У цветковых растений часто встречаются радиальносимметричные цветки: 3 плоскости симметрии (водокрас лягушачий), 4 плоскости симметрии (лапчатка прямая), 5 плоскостей симметрии (колокольчик), 6 плоскостей симметрии (безвременник). Цветки с радиальной симметрией называются актиноморфными, цветки с билатеральной симметрией — зигоморфными.
Иглокожие
Еще какие животные имеют лучевую симметрию? Конечно, всем известные и очень красивые, необычные и яркие иглокожие. Данный тип насчитывает порядка 7 тысяч видов этих удивительных представителей морской фауны. Выделяют пять основных классов:
- Голотурии — напоминают червей, однако все же лучевую симметрию имеют. Ярко окрашены, передвигаются неохотно по морскому дну.
- Офиуры — напоминают морских звезд, однако отличаются более высокой подвижностью и бедностью окраски — белые, молочные и бежевые цвета.
- Морские ежи — могут иметь правильный, игольчатый наружный скелет, а могут и не иметь иголок. Форма тела практически всегда близка к шарообразной.
- Морские звезды — пяти, восьми или двенадцатилучевые животные с явно выраженной радиальной симметрией. Очень красиво окрашены, образ жизни ведут малоподвижный, ползают по дну.
- Морские лилии — сидячие красивые животные, имеют форму радиального цветка. Могут отделяться от субстрата и передвигаться на более богатые пищей места.
Образ жизни может быть как подвижным, так прикрепленным (морские лилии). Тело двухслойное, ротовое отверстие выполняет функцию анального и полового. Наружный скелет достаточно прочный, известковый, красиво украшен цветными узорами.
Личинки этих животных имеют билатеральную симметрию тела, и только взрослые особи доращивают лучи до радиальности.
Биология
В биологии о радиальной симметрии говорят, когда через трёхмерное существо проходят одна или более осей симметрии. При этом радиальносимметричные животные могут и не иметь плоскостей симметрии. Так, у сифонофоры Velella имеется ось симметрии второго порядка и нет плоскостей симметрии.
Обычно через ось симметрии проходят две или более плоскости симметрии. Эти плоскости пересекаются по прямой — оси симметрии. Если животное будет вращаться вокруг этой оси на определённый градус, то оно будет отображаться само на себе (совпадать само с собой).
Таких осей симметрии может быть несколько (полиаксонная симметрия) или одна (монаксонная симметрия). Полиаксонная симметрия распространена среди протистов (например, радиолярий).
Как правило, у многоклеточных животных два конца (полюса) единственной оси симметрии неравноценны (например, у медуз на одном полюсе (оральном) находится рот, а на противоположном (аборальном) — верхушка колокола. Такая симметрия (вариант радиальной симметрии) в сравнительной анатомии называется одноосно-гетеропольной. В двухмерной проекции радиальная симметрия может сохраняться, если ось симметрии направлена перпендикулярно к проекционной плоскости. Иными словами, сохранение радиальной симметрии зависит от угла наблюдения.
Радиальная симметрия характерна для многих стрекающих, а также для большинства иглокожих. Среди них встречается так называемая пентасимметрия, базирующаяся на пяти плоскостях симметрии. У иглокожих радиальная симметрия вторична: их личинки двустороннесимметричны, а у взрослых животных наружная радиальная симметрия нарушается наличием мадрепоровой пластинки.
Кроме типичной радиальной симметрии существует двулучевая радиальная симметрия (две плоскости симметрии, к примеру, у гребневиков). Если плоскость симметрии только одна, то симметрия билатеральная (такую симметрию имеют животные из группы Bilateria).
У цветковых растений часто встречаются радиальносимметричные цветки: 3 плоскости симметрии (водокрас лягушачий), 4 плоскости симметрии (лапчатка прямая), 5 плоскостей симметрии (колокольчик), 6 плоскостей симметрии (безвременник). Цветки с радиальной симметрией называются актиноморфными, цветки с билатеральной симметрией — зигоморфными.
Элементы симметрии
Среди элементов симметрии различают следующие:
- плоскость симметрии — плоскость, делящая объект на две равные (зеркально симметричные) половины;
- ось симметрии — прямая линия, при повороте вокруг которой на некоторый угол, меньший 360о, объект совпадает сам с собой;
- центр симметрии — точка, делящая пополам все прямые линии, соединяющие подобные точки объекта.
Обычно через центр симметрии проходят оси симметрии, а через ось симметрии — плоскости симметрии. Однако существуют тела и фигуры, у которых при наличии центра симметрии нет ни осей, ни плоскостей симметрии, а при наличии оси симметрии отсутствуют плоскости симметрии (см. ниже).
Кроме этих геометрических элементов симметрии, различают биологические:
- антимеры — симметрично повторяющиеся вокруг главной оси монаксонно гетерополярных (см. ниже) форм участки тела;
- радиус — плоскость симметрии антимер;
- интеррадиус — плоскость, проходящая между соседними антимерами;
- метамеры — повторяющиеся участки, расположенные вдоль продольной (обычно передне-задней) оси тела организма.
Типы симметрий
У биологических объектов встречаются следующие типы симметрии:
- сферическая симметрия — симметричность относительно вращений в трёхмерном пространстве на произвольные углы.
-
аксиальная симметрия (радиальная симметрия
симметрия вращения n-го порядка — симметричность относительно поворотов на угол 360°/n вокруг какой-либо оси.
, симметрия вращения неопределённого порядка) — симметричность относительно поворотов на произвольный угол вокруг какой-либо оси.
- двусторонняя (билатеральная) симметрия — симметричность относительно плоскости симметрии (симметрия зеркального отражения).
- трансляционная симметрия — симметричность относительно сдвигов пространства в каком-либо направлении на некоторое расстояние (её частный случай у животных — метамерия (биология)).
- триаксиальная асимметрия — отсутствие симметрии по всем трём пространственным осям.
Классификация типов симметрии цветков растений
| Тип симметрии | Плоскости симметрии | Синонимы | Примеры |
|---|---|---|---|
| Древняя асимметрия или гапломорфия | Нет | Актиноморфия, радиальная, регулярная | Магнолия (Magnoliaceae), Нимфея (Nymphaceae) |
| Актиноморфия или радиальная симметрия | Обычно больше двух (полисимметричные) | Регулярная, плеоморфия, стереоморфия, мультисимметрия | Примула (Primulaceae), Нарцисс (Amaryllidaceae), Pyrola (Ericaceae) |
| Дисимметрия | Две (дисимметричные) | Билатеральная симметрия | Dicentra (Fumariaceae) |
| Зигоморфия | Одна (моносимметричные) | Билатеральная, нерегулярная, медиальная зигоморфия | |
| Salvia (Lamiaceae), Орхидея (Orchidaceae), Scrophularia (Scrophulariaceae) | |||
| Fumaria и Corydalis (Fumariaceae) | |||
| Облигатная зигоморфия | Aesculus (Hippocastanaceae) находят у Malpighiaceae, Sapindaceae | ||
| Приобретённая асимметрия | Нет | Нерегулярная, асимметрия | |
| Нерегулярная, асимметрия | Centranthus (Valerianaceae), находят у Cannaceae, Fabaceae, Marantaceae, Zingiberaceae | ||
|
Энантиостилия, неравнолатеральная | Cassia (Caeasalpinaceae), Cyanella (Tecophilaeceae), Monochoria (Pontederiaceae), Solanum (Solanaceae), Barberetta и Wachendorffia (Haemodoraceae) |
Симметрия в геометрии
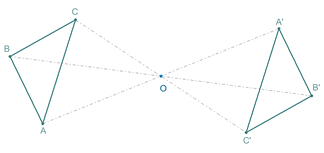
Два треугольника с точечной симметрией отражения в плоскости. Треугольник А’В’С может быть получен из треугольника ABC поворотом на 180 ° вокруг точки O.
Геометрическая симметрия — это наиболее известный тип симметрии для многих людей. Геометрический объект называется симметричным, если после того как он был преобразован геометрически, он сохраняет некоторые исходные свойства. Например, круг, повёрнутый вокруг своего центра, будет иметь ту же форму и размер, что и исходный круг. Поэтому круг называется симметричным относительно вращения (имеет осевую симметрию).
Виды симметрий, возможных для геометрического объекта, зависят от множества доступных геометрических преобразований и того, какие свойства объекта должны оставаться неизменными после преобразования.
Виды геометрических симметрий:
- Зеркальная симметрия
- Осевая симметрия
- Вращательная симметрия
- Центральная симметрия
- Скользящая симметрия
- Винтовая симметрия
Зеркальная симметрия
Зеркальная симметрия или отражение— движение евклидова пространства, множество неподвижных точек которого является гиперплоскостью (в случае трехмерного пространства — просто плоскостью). Термин зеркальная симметрия употребляется также для описания соответствующего типа симметрии объекта, то есть, когда объект при операции отражения переходит в себя. Это математическое понятие в оптике описывает соотношение объектов и их (мнимых) изображений при отражении в плоском зеркале. Проявляется во многих законах природы (в кристаллографии, химии, физике, биологии и т. д., а также в искусстве и искусствоведении).
Осевая симметрия
Фигура называется симметричной относительно прямой А, если для каждой точки фигуры симметричная ей точка относительно прямой А также принадлежит этой фигуре.
Вращательная симметрия
Вращательная симметрия — термин, означающий симметрию объекта относительно всех или некоторых собственных вращений m-мерного евклидова пространства. Собственными вращениями называются разновидности изометрии, сохраняющие ориентацию. Таким образом, группа симметрии, отвечающая вращениям, есть подгруппа группы E+(m) (см. Евклидова группа).
Трансляционная симметрия может рассматриваться как частный случай вращательной — вращение вокруг бесконечно-удалённой точки. При таком обобщении группа вращательной симметрии совпадает с полной E+(m). Такого рода симметрия неприменима к конечным объектам, поскольку делает всё пространство однородным, однако она используется в формулировке физических закономерностей.
Совокупность собственных вращений вокруг фиксированной точки пространства образуют специальную ортогональную группу SO(m) — группу ортогональных матриц m×m с определителем, равным 1. Для частного случая m = 3 группа носит специальное название — группа вращений.
В физике инвариантность относительно группы вращений называется изотропностью пространства (все направления в пространстве равноправны) и выражается в инвариантности физических законов, в частности, уравнений движения, относительно вращений. Теорема Нётер связывает эту инвариантность с наличием сохраняющейся величины (интеграла движения) — углового момента.
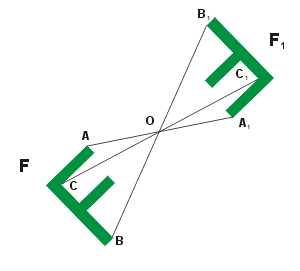
Центральная симметрия
Симметрия относительно точки
Центра́льной симме́трией (иногда центра́льной инве́рсией) относительно точки A называют преобразование пространства, переводящее точку X в такую точку X′, что A — середина отрезка XX′. Центральная симметрия с центром в точке A обычно обозначается через ZA{\displaystyle Z_{A}}, в то время как обозначение SA{\displaystyle S_{A}} можно перепутать с осевой симметрией. Фигура называется симметричной относительно точки A, если для каждой точки фигуры симметричная ей точка относительно точки A также принадлежит этой фигуре. Точка A называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией. Другие названия этого преобразования — симметрия с центром A. Центральная симметрия в планиметрии является частным случаем поворота, точнее, является поворотом на 180 градусов.
Скользящая симметрия
Скользящая симметрия — изометрия евклидовой плоскости.
Скользящей симметрией называют композицию симметрии относительно некоторой прямой l{\displaystyle l} и переноса на вектор, параллельный l{\displaystyle l} (этот вектор может быть и нулевым). Скользящую симметрию можно представить в виде композиции 3 осевых симметрий (теорема Шаля).
Симметрия в религии и культуре
Предполагается, что тенденция людей видеть цель в симметрии, является одной из причин, почему симметрия часто является неотъемлемой частью символов мировых религий. Вот лишь некоторые из многих примеров, изображённые на рисунке справа.
Люди наблюдают симметричную природу (также включающую асимметричный баланс) социального взаимодействия в различных контекстах. Они включают оценки взаимности, эмпатии, извинения, диалога, уважения, справедливости и мести. Симметричные взаимодействия посылают сигналы «мы одинаковые», а асимметричные взаимодействия выражают мысль «я особый, лучше, чем ты». Взаимоотношения со сверстниками строятся на основе симметрии, а властные отношения — на асимметрии.
Загадка кораллов
Мы уже сказали, что стрекающие и билатерии — ближайшие родственники. Иными словами, они равноправные потомки некоего предка, общего только для этих двух групп. Такие группы называются сестринскими. Очевидно, что быть предками или потомками друг друга сестринские группы не могут по определению. И в самом деле, стрекающие и билатерии появляются в палеонтологической летописи приблизительно одновременно — в конце вендского периода (см. A. Y. Ivantsov, M. A. Fedonkin, 2002. Conulariid–like fossil from the Vendian of Russia: a metazoan clade across the Proterozoic/Palaeozoic boundary). Считать, что стрекающие примитивнее билатерий, нет никаких оснований, ровно так же, как нет никаких оснований и для обратного.
Но как же был устроен общий предок билатерий и стрекающих? Палеонтология ответить на этот вопрос пока не может. Значит, дело за сравнительным исследованием современных животных. Что могут нам «сообщить» стрекающие в свете сравнения с билатериями?
Стрекающие — крупная группа животных, в состав которой входит больше 10 000 современных видов. Они бывают очень разными. Крохотная пресноводная гидра совсем не похожа на роскошных медуз или на невзрачных строителей громадных коралловых рифов. Тем не менее можно утверждать, что все стрекающие делятся всего лишь на два эволюционных ствола (рис. 1). Ствол Anthozoa — это коралловые полипы, донные животные, никогда не имеющие в своем развитии стадии медузы. Ствол Medusozoa состоит из животных, у которых стадии медузы и полипа, как правило, чередуются в одном и том же жизненном цикле. У некоторых Medusozoa или стадия медузы, или стадия полипа могут отсутствовать, но это — случаи вторичной утраты. Судя по всему, «изобретение» жизненной формы медузы и соответствующего типа жизненного цикла было важнейшим в истории стрекающих эволюционным новшеством. А положение ствола Anthozoa на эволюционном древе позволяет думать, что именно он сохранил самые древние признаки. Более того, есть работы, где предполагается, что Anthozoa — вовсе не ствол, а эволюционный уровень, охватывающий всех древнейших стрекающих (E. Kayal et al., 2013. Cnidarian phylogenetic relationships as revealed by mitogenomics). Так или иначе, примитивность этих животных несомненна.
Коралловые полипы сами по себе довольно разнообразны (число их видов превосходит число видов всех Medusozoa, вместе взятых). Они бывают одиночными или колониальными, бывают прикрепленными или подвижными, как, например, популярная у биологов развития хищная актиния нематостелла. Тем не менее у всех коралловых полипов можно выделить как минимум две общие особенности, важные для нашей темы (рис. 2).
Во-первых, перед входом в кишечную полость кораллового полипа всегда находится трубчатая глотка, отчетливо сплющенная в одной плоскости. Просвет такой глотки представляет собой более или менее широкую щель. У многих видов щелевидным становится и рот — это видно снаружи.
Во-вторых, кишечная полость кораллового полипа разделена врастающими со стороны стенок перегородками — септами — на несколько частично замкнутых камер. Точное число камер соответствует числу щупалец, окружающих рот. Некоторые авторы считали эти камеры предшественниками целомических полостей двусторонне-симметричных животных (они действительно образуются похожим способом).
Наш известный зоолог Владимир Васильевич Малахов в свежем обзоре обращает внимание на то, что внутренняя симметрия тела коралловых полипов не является радиальной. На самом деле их симметрия — двусторонняя
Особенно хорошо это заметно у одиночных шестилучевых кораллов из группы цериантарий. Щелевидный рот цериантарий ведет в сплющенную глотку, плоскость которой служит плоскостью двусторонней симметрии всего животного. На одном узком конце глотки находится сифоноглиф — продольный желобок, выстланный клетками с ресничками и предназначенный для тока воды. Вблизи другого узкого конца глотки расположена зона роста, в которой образуются новые септы. Сторону полипа, где у цериантарий находится сифоноглиф, по традиции называют «спинной», а сторону, где находится зона роста, «брюшной». Это полноценная двусторонняя симметрия — как у билатерий.
В других группах коралловых полипов картина усложняется (например, может появляться второй сифоноглиф), но внутренняя двусторонняя симметрия, определяемая плоскостью глотки, сохраняется у них всегда. По утверждению Малахова, она есть абсолютно у всех представителей Anthozoa. А вот у Medusuzoa ее, как правило, не бывает, там симметрия чисто радиальная.
Элементы симметрии
Среди элементов симметрии различают следующие:
- плоскость симметрии — плоскость, делящая объект на две равные (зеркально симметричные) половины;
- ось симметрии — прямая линия, при повороте вокруг которой на некоторый угол, меньший 360о, объект совпадает сам с собой;
- центр симметрии — точка, делящая пополам все прямые линии, соединяющие подобные точки объекта.
Обычно через центр симметрии проходят оси симметрии, а через ось симметрии — плоскости симметрии. Однако существуют тела и фигуры, у которых при наличии центра симметрии нет ни осей, ни плоскостей симметрии, а при наличии оси симметрии отсутствуют плоскости симметрии (см. ниже).
Кроме этих геометрических элементов симметрии, различают биологические:
- антимеры — симметрично повторяющиеся вокруг главной оси монаксонно гетерополярных (см. ниже) форм участки тела;
- радиус — плоскость симметрии антимер;
- интеррадиус — плоскость, проходящая между соседними антимерами;
- метамеры — повторяющиеся участки, расположенные вдоль продольной (обычно передне-задней) оси тела организма.
Эволюция симметрии
Признаки симметрии определяются внешней средой. Полностью изотропной экологической нише соответствует максимальная степень симметрии организмов. Первые организмы на Земле, плавающие в толще воды одноклеточные, возможно, имели максимально возможную симметрию — шаровую, они появились примерно 3.5 млрд лет назад.
Эволюция симметрии у животных и протистов
Высшие животные — пример билатеральной симметрии
Вольвокс — пример сферической симметрии
Асимметризация у животных по оси «верх-низ» происходила под действием поля гравитации. Это привело к появлению брюшной (нижней) и спинной (верхней) стороны у подавляющего большинства подвижных животных (как с радиальной, так и билатеральной симметрией). У некоторых радиальносимметричных сидячих животных нет спинной и брюшной стороны, нижней стороне тела обычно соответствует аборальный полюс, верхней — оральный (ротовой).
Асимметризация по передне-задней оси происходила при взаимодействии с пространственным полем, когда понадобилось быстрое движение (спастись от хищника, догнать жертву). В результате в передней части тела оказались главные рецепторы и мозг.
Билатерально симметричные многоклеточные животные господствуют последние 600—535 млн лет. Они стали окончательно преобладающими в фауне Земли после «кембрийского взрыва». До этого, среди представителей вендской фауны, преобладали радиальносимметричные формы и своеобразные животные, обладавшие «симметрией скользящего отражения», например, чарния.
Среди современных животных первично радиальной симметрией, по-видимому, обладают только губки и гребневики; хотя стрекающие и относятся к радиальносимметричным животным, симметрия у коралловых полипов обычно билатеральная. По современным молекулярным данным, симметрия у стрекающих, вероятно, исходно была билатеральной, а радиальная симметрия, свойственная медузозоям, вторична.
В. Н. Беклемишев в своём классическом труде дал подробный анализ элементов симметрии и подробную классификацию типов симметрии протистов. Среди форм тела, свойственных этим организмам, он различал следующие:
- анаксонная — например, у амёб (полная асимметрия);
- сферическая (шаровая симметрия, имеется центр симметрии, в котором пересекается бесконечное число осей симметрии бесконечно большого порядка) — например, у многих спор или цист;
- неопределенно полиаксонная (есть центр симметрии и конечное, но неопределённое число осей и плоскостей) — многие солнечники;
- правильная полиаксонная (строго определённое число осей симметрии определённого порядка) — многие радиолярии;
- ставраксонная (монаксонная) гомополярная (есть одна ось симметрии с равноценными полюсами, то есть пересекаемая в центре плоскостью симметрии, в которой лежат не менее двух дополнительных осей симметрии) — некоторые радиолярии;
- монаксонная гетерополярная (есть одна ось симметрии с двумя неравноценными полюсами, центр симметрии исчезает) — многие радиолярии и жгутиковые, раковинные корненожки, грегарины, примитивные инфузории;
- билатеральная — дипломонады, бодониды, фораминиферы.
Эти формы симметрии перечислены в том порядке, в котором Беклемишев выстроил их в морфологический ряд. Считая полностью асимметричную амёбу более примитивным существом, чем одноклеточные организмы с шаровой симметрией (радиолярии, вольвоксовые), он поместил её в начало ряда. Билатерально симметричные организмы являются конечным звеном этого морфологического ряда, который, конечно, не является эволюционным (Беклемишев подчёркивает, что билатеральная симметрия может возникать независимо самыми разными путями).
Другой морфологический ряд, рассмотренный в той же работе — ряд форм с вращательной симметрией (это такой тип симметрии, при которой имеется только ось симметрии и отсутствуют плоскости симметрии).
Анализируя связь симметрии со средой обитания, Беклемишев связывает полиаксонную форму тела с однородностью среды, монаксонно гетерополярную — с прикреплением к субстрату, вращательную (винтовую) — со способом передвижения многих протистов («ввинчивание» в воду). Билатеральная симметрия многоклеточных животных, по Беклемишеву, возникла в связи с ползанием по дну.
Симметрии в физике
Основная статья: Симметрия (физика)
| Симметрия в физике | ||
|---|---|---|
| Преобразование | Соответствующаяинвариантность | Соответствующийзаконсохранения |
| Трансляции времени | Однородностьвремени | …энергии |
| ⊠ C, P, CP и T-симметрии | Изотропностьвремени | …чётности |
| Трансляции пространства | Однородностьпространства | …импульса |
| ↺ Вращения пространства | Изотропностьпространства | …моментаимпульса |
| ⇆ Группа Лоренца (бусты) | ОтносительностьЛоренц-ковариантность | …движенияцентра масс |
| ~ Калибровочное преобразование | Калибровочная инвариантность | …заряда |
В теоретической физике поведение физической системы описывается некоторыми уравнениями. Если эти уравнения обладают какими-либо симметриями, то часто удаётся упростить их решение путём нахождения сохраняющихся величин (интегралов движения). Так, уже в классической механике формулируется теорема Нётер, которая каждому типу непрерывной симметрии сопоставляет сохраняющуюся величину. Из неё, например, следует, что инвариантность уравнений движения тела с течением времени приводит к закону сохранения энергии; инвариантность относительно сдвигов в пространстве — к закону сохранения импульса; инвариантность относительно вращений — к закону сохранения момента импульса.
Суперсимметрия
Суперсимме́трия или симме́трия Ферми́ — Бозе́ — гипотетическая симметрия, связывающая бозоны и фермионы в природе. Абстрактное преобразование суперсимметрии связывает бозонное и фермионное квантовые поля, так что они могут превращаться друг в друга. Образно можно сказать, что преобразование суперсимметрии может переводить вещество во взаимодействие (или в излучение), и наоборот.
По состоянию на начало 2009 года суперсимметрия является физической гипотезой, не подтверждённой экспериментально. Совершенно точно установлено, что наш мир не является суперсимметричным в смысле точной симметрии, так как в любой суперсимметричной модели фермионы и бозоны, связанные суперсимметричным преобразованием, должны обладать одинаковыми массой, зарядом и другими квантовыми числами (за исключением спина). Данное требование не выполняется для известных в природе частиц. Предполагается, тем не менее, что существует энергетический лимит, за пределами которого поля подчиняются суперсимметричным преобразованиям, а в рамках лимита — нет. В таком случае частицы-суперпартнёры обычных частиц оказываются очень тяжёлыми по сравнению с обычными частицами. Поиск суперпартнёров обычных частиц — одна из основных задач современной физики высоких энергий. Ожидается, что Большой адронный коллайдер сможет открыть и исследовать суперсимметричные частицы, если они существуют, или поставить под большое сомнение суперсимметричные теории, если ничего не будет обнаружено.
Трансляционная симметрия
Трансляционная симметрия — тип симметрии, при которой свойства рассматриваемой системы не изменяются при сдвиге на определённый вектор, который называется вектором трансляции. Например, однородная среда совмещается сама с собой при сдвиге на любой вектор, поэтому для неё свойственна трансляционная симметрия.
Трансляционная симметрия свойственна также для кристаллов. В этом случае векторы трансляции не произвольны, хотя их существует бесконечное число. Среди всех векторов трансляций кристаллической решётки можно выбрать 3 таким образом, что любой другой вектор трансляции был бы целочисленно-линейной комбинацией этих трёх векторов. Эти три вектора составляют базис кристаллической решётки.
Теория групп показывает, что трансляционная симметрия в кристаллах совместима только с поворотами на углы θ=2π/n, где n может принимать значения 1, 2, 3, 4, 6.
При повороте на углы 180, 120, 90, 60 градусов положение атомов в кристалле не меняется. Говорят, что кристаллы имеют ось вращения n-го порядка.[уточнить]
Перенос в плоском четырёхмерном пространстве-времени не меняет физических законов. В теории поля трансляционная симметрии, согласно теореме Нётер, соответствует сохранению тензора энергии-импульса. В частности, чисто временные трансляции соответствуют закону сохранения энергии, а чисто пространственные сдвиги — закону сохранения импульса.
Биология
В биологии о радиальной симметрии говорят, когда через трёхмерное существо проходят одна или более осей симметрии. При этом радиальносимметричные животные могут и не иметь плоскостей симметрии. Так, у сифонофоры Velella имеется ось симметрии второго порядка и нет плоскостей симметрии.
Обычно через ось симметрии проходят две или более плоскости симметрии. Эти плоскости пересекаются по прямой — оси симметрии. Если животное будет вращаться вокруг этой оси на определённый градус, то оно будет отображаться само на себе (совпадать само с собой).
Таких осей симметрии может быть несколько (полиаксонная симметрия) или одна (монаксонная симметрия). Полиаксонная симметрия распространена среди протистов (например, радиолярий).
Как правило, у многоклеточных животных два конца (полюса) единственной оси симметрии неравноценны (например, у медуз на одном полюсе (оральном) находится рот, а на противоположном (аборальном) — верхушка колокола. Такая симметрия (вариант радиальной симметрии) в сравнительной анатомии называется одноосно-гетеропольной. В двухмерной проекции радиальная симметрия может сохраняться, если ось симметрии направлена перпендикулярно к проекционной плоскости. Иными словами, сохранение радиальной симметрии зависит от угла наблюдения.
Радиальная симметрия характерна для многих стрекающих, а также для большинства иглокожих. Среди них встречается так называемая пентасимметрия, базирующаяся на пяти плоскостях симметрии. У иглокожих радиальная симметрия вторична: их личинки двустороннесимметричны, а у взрослых животных наружная радиальная симметрия нарушается наличием мадрепоровой пластинки.
Кроме типичной радиальной симметрии существует двулучевая радиальная симметрия (две плоскости симметрии, к примеру, у гребневиков). Если плоскость симметрии только одна, то симметрия билатеральная (такую симметрию имеют животные из группы Bilateria).
У цветковых растений часто встречаются радиальносимметричные цветки: 3 плоскости симметрии (водокрас лягушачий), 4 плоскости симметрии (лапчатка прямая), 5 плоскостей симметрии (колокольчик), 6 плоскостей симметрии (безвременник). Цветки с радиальной симметрией называются актиноморфными, цветки с билатеральной симметрией — зигоморфными.
Типы симметрий
У биологических объектов встречаются следующие типы симметрии:
- сферическая симметрия — симметричность относительно вращений в трёхмерном пространстве на произвольные углы.
-
аксиальная симметрия (радиальная симметрия
симметрия вращения n-го порядка — симметричность относительно поворотов на угол 360°/n вокруг какой-либо оси.
, симметрия вращения неопределённого порядка) — симметричность относительно поворотов на произвольный угол вокруг какой-либо оси.
- двусторонняя (билатеральная) симметрия — симметричность относительно плоскости симметрии (симметрия зеркального отражения).
- трансляционная симметрия — симметричность относительно сдвигов пространства в каком-либо направлении на некоторое расстояние (её частный случай у животных — метамерия (биология)).
- триаксиальная асимметрия — отсутствие симметрии по всем трём пространственным осям.
Классификация типов симметрии цветков растений
| Тип симметрии | Плоскости симметрии | Синонимы | Примеры |
|---|---|---|---|
| Древняя асимметрия или гапломорфия | Нет | Актиноморфия, радиальная, регулярная | Магнолия (Magnoliaceae), Нимфея (Nymphaceae) |
| Актиноморфия или радиальная симметрия | Обычно больше двух (полисимметричные) | Регулярная, плеоморфия, стереоморфия, мультисимметрия | Примула (Primulaceae), Нарцисс (Amaryllidaceae), Pyrola (Ericaceae) |
| Дисимметрия | Две (дисимметричные) | Билатеральная симметрия | Dicentra (Fumariaceae) |
| Зигоморфия | Одна (моносимметричные) | Билатеральная, нерегулярная, медиальная зигоморфия | |
| Salvia (Lamiaceae), Орхидея (Orchidaceae), Scrophularia (Scrophulariaceae) | |||
| Fumaria и Corydalis (Fumariaceae) | |||
| Облигатная зигоморфия | Aesculus (Hippocastanaceae) находят у Malpighiaceae, Sapindaceae | ||
| Приобретённая асимметрия | Нет | Нерегулярная, асимметрия | |
| Нерегулярная, асимметрия | Centranthus (Valerianaceae), находят у Cannaceae, Fabaceae, Marantaceae, Zingiberaceae | ||
|
Энантиостилия, неравнолатеральная | Cassia (Caeasalpinaceae), Cyanella (Tecophilaeceae), Monochoria (Pontederiaceae), Solanum (Solanaceae), Barberetta и Wachendorffia (Haemodoraceae) |













